[專題演講] 【7月5日】法國格勒諾貝爾-阿爾卑斯大學 謝宇觀博士候選人

Speaker: 謝宇觀 (Yu-Guan Hsieh)博士候選人 (法國格勒諾貝爾-阿爾卑斯大學, University of Grenoble Alpes, France)

專長: Online learning, Distributed optimization, Learning in games

個人網站:
https://www.cyber-meow.com/

Title: Anticipating the future for better performance: Optimistic gradient algorithms for learning in games

Abstract:
Recent advances in machine learning have called for the need for optimization beyond the minimization of a single loss function. This includes, for example, multi-agent reinforcement learning and the training of generative adversarial networks. In these problems, multiple learners are ‌in competition or in collaboration, and the “solution” of the problem can often be encoded by the equilibrium of a game. Meanwhile, the interplay between the dynamic and the static solution concepts of games has been an intriguing problem in the field of game theory for decades, and the study of various learning-in-game dynamics has particularly gained popularity in the past few years.

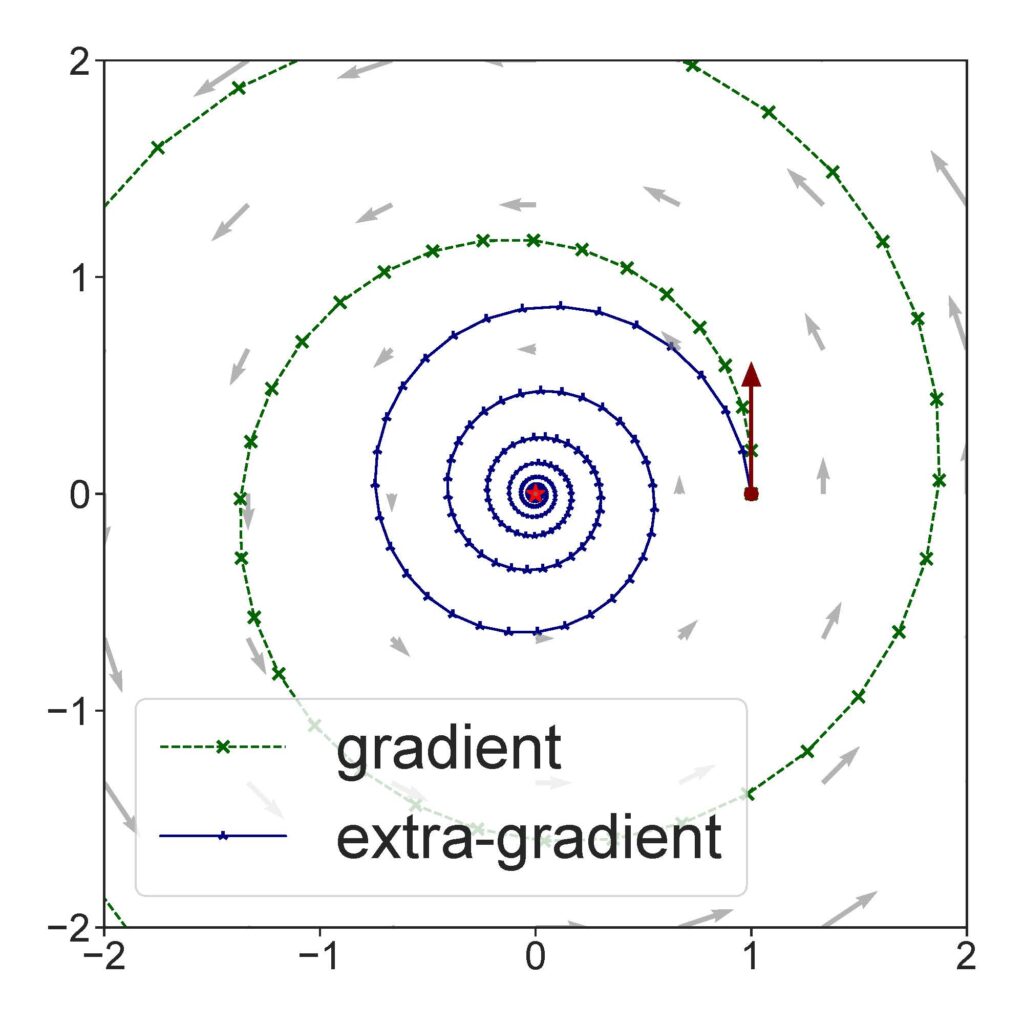
In this talk, we will focus on optimistic gradient descent, a family of algorithms that equip the vanilla gradient method with a look-ahead step. It inherits many nice properties from extra-gradient — its two-call variant — and in particular resolves the non-convergence behavior of the vanilla gradient method in bilinear games (i.e. min_{x} max_{y} xy). We will provide intuition, discuss convergence guarantees, and look into the stochastic and adaptive variants of the method that can be applied in more realistic scenarios.

Date: Tuesday, July 5, 2022

Time: 14:00-15:00

Venue: M212

Refreshment: 13:30-14:00, M104

本演講亦可線上參加

https://meet.google.com/fww-nkka-pny