課程資訊
- [課程資訊] 本校113學年度第1學期期中課程意見調查 2024-10-21
- [課程資訊] 113-1停修辦理日期:113年10月14日(一)至112年11月22日(五) 2024-10-16
- [課程資訊] 113學年度第1學期超修及學分不足申請、二一選課輔導期限為9/20(五) 2024-09-03
- [課程資訊] 數學系113學年度第1學期學分抵免、採認辦理注意事項 2024-08-26
- [課程資訊] 本系113學年度大學部新生選課說明 2024-08-20
課程規劃
課程規劃
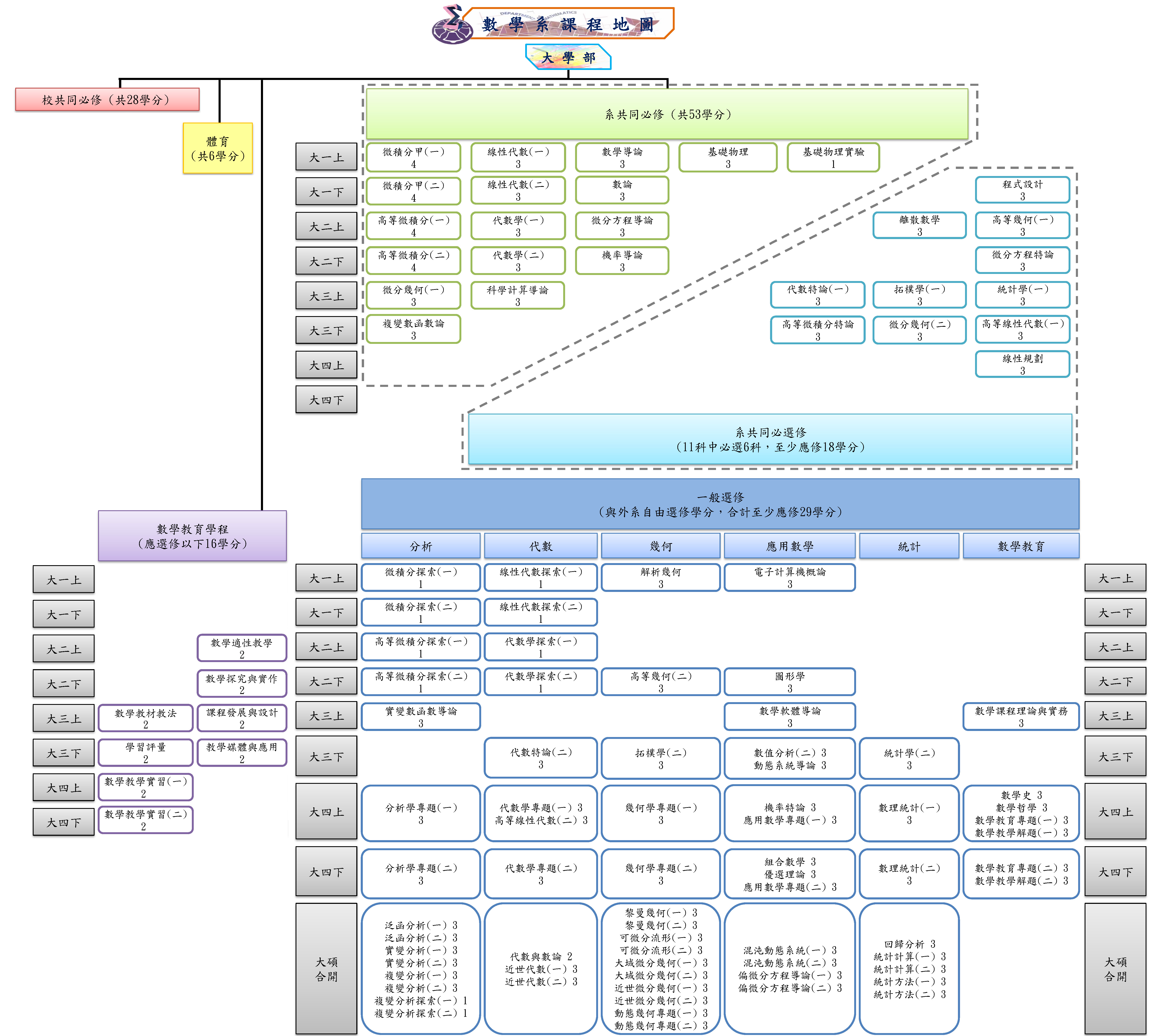
本系學士班辦學的主要目標為培育良好數學專業、應用數學及數學教育研究人才、培育中學及大學之優良數學師資、培養能將數學應用於各方面的人才。基於此種需要,本系對於學士班學生之修習科目以橫向與縱向兩個面向來進行課程規劃。
橫向面向著重在學生於各領域之間的平衡發展與相互之間的連結,同時從中發掘自己的專長領域,以供為來繼續深造。領域區分以本系之五大課程領域為依歸,分別 是:分析、代數、幾何、應用數學、數學教育領域,其中應用數學領域又分成微分方程、電腦與計算、組合學、優選理論和統計等五個子領域。
縱向面向則以學生的學習發展層次為準,又可分成「專業課程導向」與「職能導向」兩個類型,其中專業課程導向又劃分成三個面向,職能導向則分成兩個面向。每個面向各有其學習發展的層次。
數學專業課程導向的類型上的三個面向分述如下:
 數學專門科目+
數學專門科目+ 教育學分,而是
教育學分,而是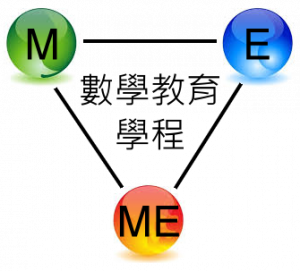 其中
其中 是指培育數學教師專用的數學教育科目,像數學適性教學、數學探究與實作、學習評量、教學媒體與運用、課程發展與設計、數學教材教法、數學教學實習、數學史等。
是指培育數學教師專用的數學教育科目,像數學適性教學、數學探究與實作、學習評量、教學媒體與運用、課程發展與設計、數學教材教法、數學教學實習、數學史等。
1.培育數學專門能力的基本數學科目:
這類科目為本系必修課程,專為本系學生奠定數學專業基礎的課程,包含:數學導論、微積分、高等微積分、複變數函數導論、線性代數、數論、代數學、微分幾何、 微分方程導論、機率導論、科學計算導論等,範圍涵蓋分析、代數、幾何、與應用數學等領域的專業基礎課程。本面向的課程依層次供學生分別在一~三年級修讀。2.輔助數學專門能力的數學演習科目:
對於數學基本課程,本系額外開設一些輔助的課程,這些課程之主要目的,在於讓學生親身經歷這些基礎課程解題的思維歷程,以達到對課程理論、法則的熟練,進而應用解決相關之問題。目前所有必修科目皆安排探索課程,包含:微積分探索、線性代數探索、複變分析探索等。3.加強數學專門能力的數學選修科目:
本系規劃更具深度與廣度的數學選修科目,除了能延續基礎數學科目往更深的數學知識探究,也提供轉往數學之應用面向。這些科目包含初階、進階與高階課程: (1)初階選修課程:圖形學、電子計算機概論、離散數學、程式設計、高等幾何(一)等,大多開設在一、二年級供學生選讀; (2)進階選修課程:高等微積分特論、微分方程特論,代數特論、拓樸學、高等線性代數等課程,主要開設在三年級供學生選讀。 (3)高階選修課程:課程主要為大碩合開課程,讓有意進入研究所的學生提早修習更深的學科,如:實變分析、複變分析、泛函分析、近世代數、大域微分幾何、近代微分幾何、動態幾何專題、混沌動態系統、迴歸分析等課程。 而在職能導向的類型中,主要是下列兩個層次的科目:1.教育學程規定必須修習的教育科目:
不同於其他學校的師培課程理念,本系的數學師資培育課程並不將數學專業與教育專業分開培育,而是規劃「數學」與「教育」融合的「數學教育」課程,因此除了一般教育科目外,本系特別設計用以提昇學生的數學教學能力之教育科目,如數學適性教學、數學探究與實作、學習評量、教學媒體與運用、課程發展與設計、數學教材教法、數學教學實習等等,是專為學科教學知識(PCK)所設計的科目。 本系所規劃的數學教育學程,並不是 數學專門科目+
數學專門科目+ 教育學分,而是
教育學分,而是 其中
其中 是指培育數學教師專用的數學教育科目,像數學適性教學、數學探究與實作、學習評量、教學媒體與運用、課程發展與設計、數學教材教法、數學教學實習、數學史等。
是指培育數學教師專用的數學教育科目,像數學適性教學、數學探究與實作、學習評量、教學媒體與運用、課程發展與設計、數學教材教法、數學教學實習、數學史等。
2.輔助學生從事各行業而加強數學本質學能的科目:
由於未來教師的培育人數將遠超過實際需求量,因此本系欲畢業生面臨職場的挑戰將越來越多。除了從事教師工作需要一些諸如高等幾何、統計學、數學教學解題等數學科目以外,若要進入資訊科技、生物科技、財金管理或精算等行業,仍需專業數學知識,如實變數函數論、作業研究、優選理論、數理統計等,以加強學生數學本質學能。3.多元模組化、學程化科目:
本系針對未來趨勢發展,將業界所需要之能力模組化、學程化,在不影響基本數學知識培養下,鼓勵學生在投入職場前,預先進行準備。並且經過業界專家學者的合作規劃,研擬出一系列科目供學生提前累積職場能量。
領域介紹
分析領域
數學分析是由微積分演進而來,在微積分發展至現代階段中,從應用中的方法總結升華為一類綜合性分析方法,且初等微積分中也包括許多數學分析的基礎概念及技巧,可以認為這些應用方法是高等微積分生成的前提。數學分析的方式和其幾何有關,不過只要任一數學空間有定義鄰域(拓撲空間)或是有針對兩物件距離的定義(度量空間),就可以用數學分析的方式進行分析。
必須修習的課程:高等微積分、實數分析、複變分析等。
必須修習的課程:高等微積分、實數分析、複變分析等。
代數領域
是一個較為基礎的數學分支。它的研究物件有許多。諸如數、數量、代數式、關係、方程式理論、代數結構等等都是代數學的研究物件。 代數的研究對象不僅是數字,還有各種抽象化的結構。例如整數集作為一個帶有加法、乘法和序關係的集合就是一個代數結構。在其中我們只關心各種關係及其性質,而對於「數本身是甚麼」這樣的問題並不關心。常見的代數結構類型有群、環、域、模、線性空間等。並且,代數是幾何的總稱,代數是還可以用任何字母代替的。
必須修習的課程:線性代數、數論、代數學、代數特論等。
必須修習的課程:線性代數、數論、代數學、代數特論等。
幾何領域
幾何學是數學的一個基礎分支,主要研究形狀、大小、圖形的相對位置等空間區域關係以及空間形式的度量。 當代的幾何學考慮流形,空間的概念比歐幾里德中的更加抽象,兩者只在極小尺寸下才彼此近似。這些空間可以加入額外的結構,因此可以考慮其長度。近代的幾何學和物理關係密切,就像偽黎曼流形和廣義相對論的關係一樣。物理理論中最年輕的弦理論也和幾何學有密切關係。
必須修習的課程:拓樸學、微分幾何等。
必須修習的課程:拓樸學、微分幾何等。
應用數學領域
以應用為目的的明確的數學理論和方法的總稱,研究如何應用數學知識到其他範疇(尤其是科學)的數學分支,可以說是純數學的相反,應用純數學中的結論擴展到物理學等其他科學中,應用數學的發展是以科學為依據,作為科學研究的後盾。包括線性代數、矩陣理論、向量分析、複變分析、微分方程、拉普拉斯變換、傅里葉分析、數值分析、概率論、數理統計、運籌學、博弈論、控制理論、組合數學、資訊理論等許多數學分支,也包括從各種應用領域中提出的數學問題的研究。而大部分應用數學是以作為物理分析的工具。計算數學有時也可視為應用數學的一部分。應用數學大部分的教學範疇都是以物理的模型為基礎進行分析,當中或許搭配了各種數學工具,就為了更貼近物理的系統。
必須修習的課程:微積分、線性代數、微分方程導論、離散數學等,依不同的分支有不同的建議修習。
必須修習的課程:微積分、線性代數、微分方程導論、離散數學等,依不同的分支有不同的建議修習。
數學教育領域
研究數學教學的實踐和方法的學科。而且,數學教育工作者也關注促進這種實踐的工具及其研究的發展。數學教育是現代社會激烈爭論的主題之一。這個術語有個歧義,它既指各地的教室里的實踐,也指新生的一個學科,它有自己的期刊,會議,等等。這方面最重要的國際組織是數學教育國際委員會。
必須修習的課程:本系數學教育專業課程、數學教育通論、數學教學解題。
必須修習的課程:本系數學教育專業課程、數學教育通論、數學教學解題。
統計領域
在資料分析的基礎上,研究測定、收集、整理、歸納和分析反映資料資料,以便給出正確訊息的科學。這一門學科自17世紀中葉產生並逐步發展起來,它廣泛地應用在各門學科,從自然科學、社會科學到人文學科,甚至被用於工商業及政府的情報決策。隨著巨量資料時代來臨,統計的面貌也逐漸改變,與資訊、計算等領域密切結合,是資料科學中的重要主軸之一。
必須修習的課程:機率導論、統計學、數理統計等。
必須修習的課程:機率導論、統計學、數理統計等。
課程地圖
課程架構